Code - Randomized Image Methodfunction h=rim(mi, so, ro, be, Np, Nr, Tw, Fc) % mi (microphone), so (source) and ro (room) are three-dimensional column vectors. % Np: samples of the RIR. % Nr: no. of random samples (Nr=0 for original IM). % Tw: samples of low-pass filter, Fc: cut-off freq. % All quantities above are in sample periods. % be: matrix of refl. coeff. [x1,y1,z1;x2,y2,z2] h=zeros(Np,1); ps=perm([0,1],[0,1],[0,1]); Rps=repmat(so,[1,8])+(2.*ps-1).*repmat(mi,[1,8]); or=floor(Np./(ro.*2))+1; rs=perm(-or(1):or(1),-or(2):or(2),-or(3):or(3)); for i=1:size(rs'); r=rs(:, i); for j=1:8; p=ps(:,j); Rp=Rps(:,j); d=norm(2*ro.*r+Rp)+1+Nr*(2*rand-1); if round(d)>Np || round(d)<1; continue; end am=be(1,:)'.^abs(r+p).*be(2,:)'.^abs(r); if Tw==0; n=round(d); else n=(max(ceil(d-Tw/2),1):min(floor(d+Tw/2),Np))'; end s=(1+cos(2*pi*(n-d)/Tw)).*sinc(Fc*(n-d))/2; s(isnan(s))=1; h(n)=h(n)+s*prod(am)/(4*pi*(d-1)); end; end; function res=perm(varargin) [res{1:nargin}]=ndgrid(varargin{1:nargin}); res=reshape(cat(nargin+1,res{:}),[],nargin)';
On the Modeling of Rectangular Geometries in Room Acoustic Simulations
IEEE/ACM Trans. Audio, Speech, Language Proc., vol. 23, no. 3, pp. 774–786, 2015.
Enzo De Sena, Niccolò Antonello, Marc Moonen, Toon van Waterschoot
KU Leuven, ESAT--STADIUS
Stadius Center for Dynamical Systems, Signal Processing and Data Analytics,
Kasteelpark Arenberg 10, 3001 Leuven, Belgium
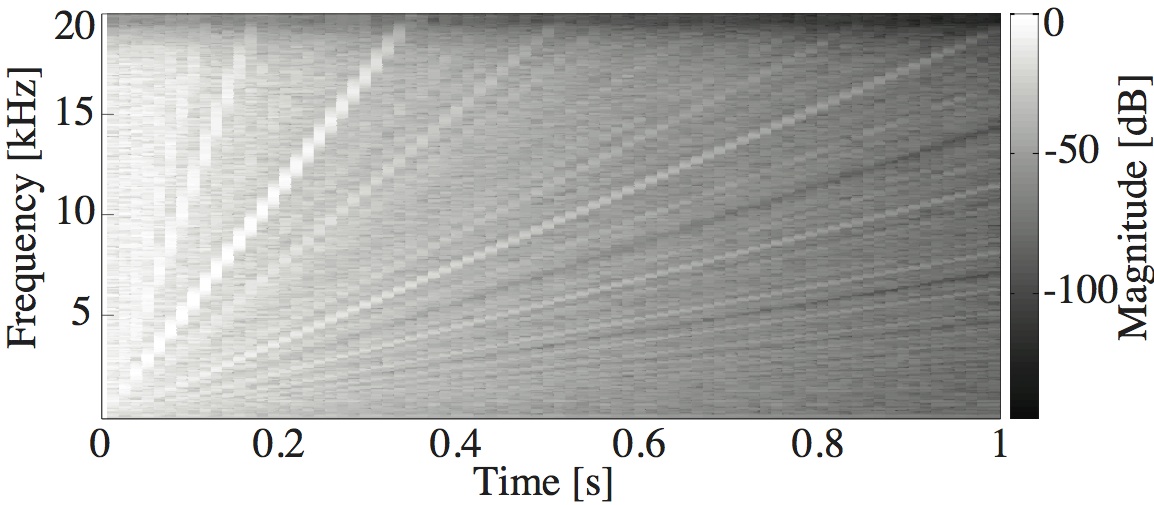
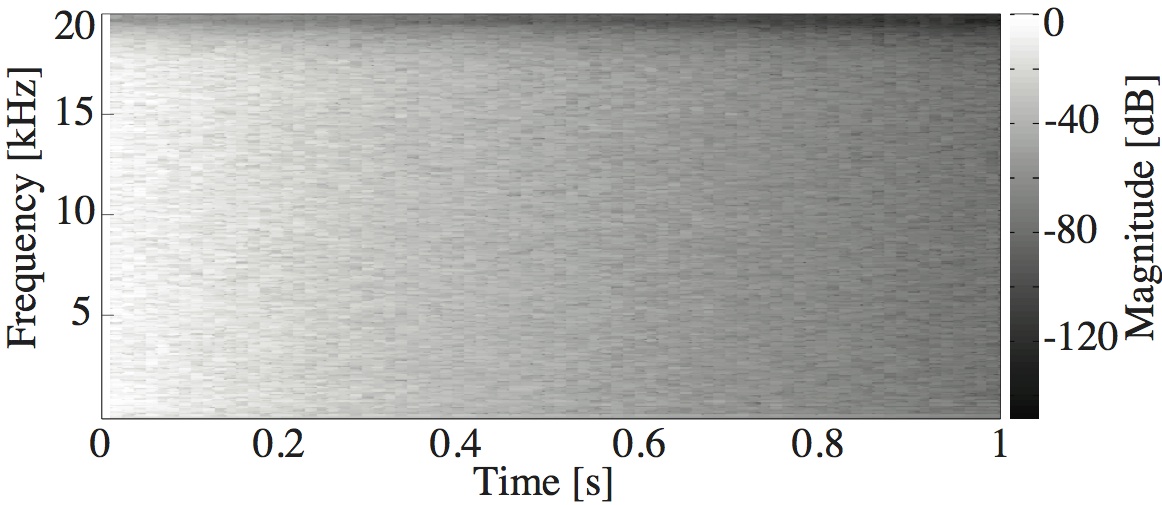
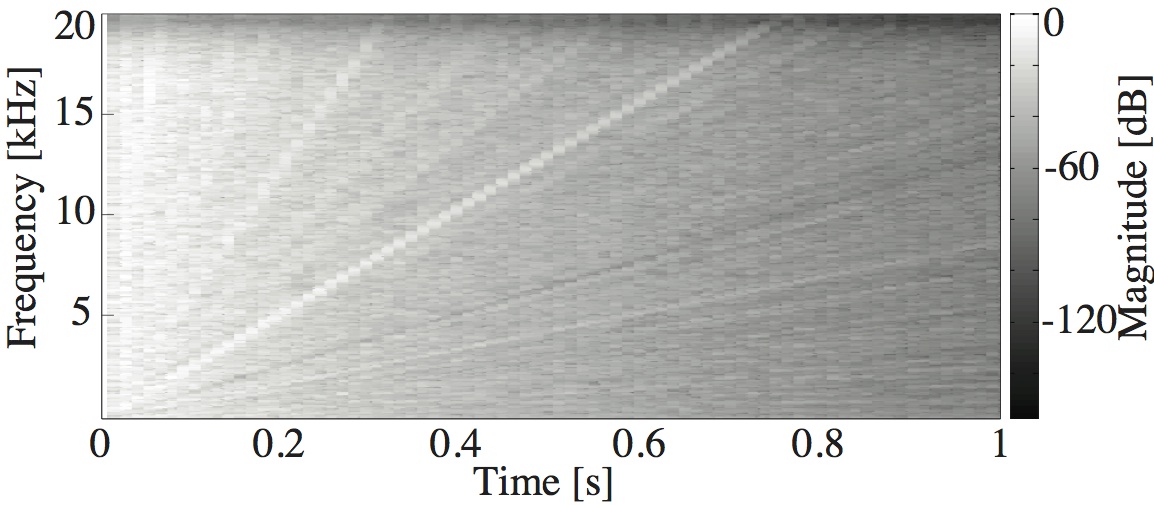
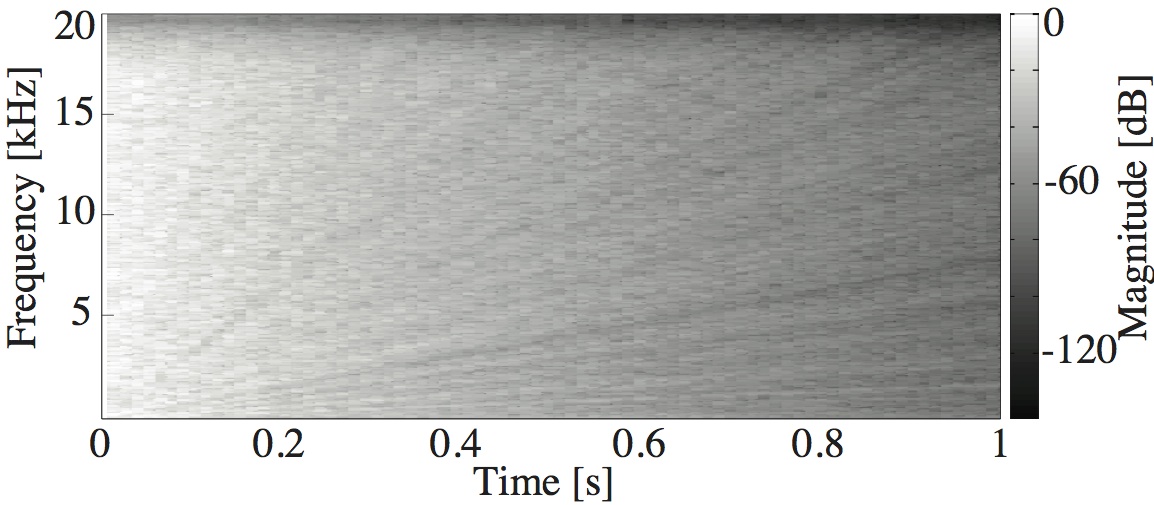
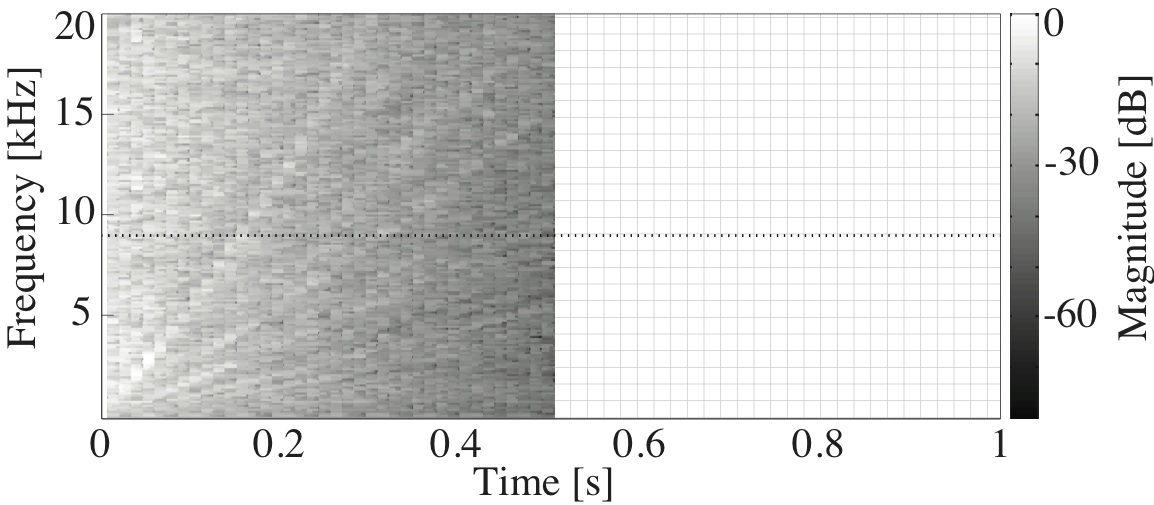
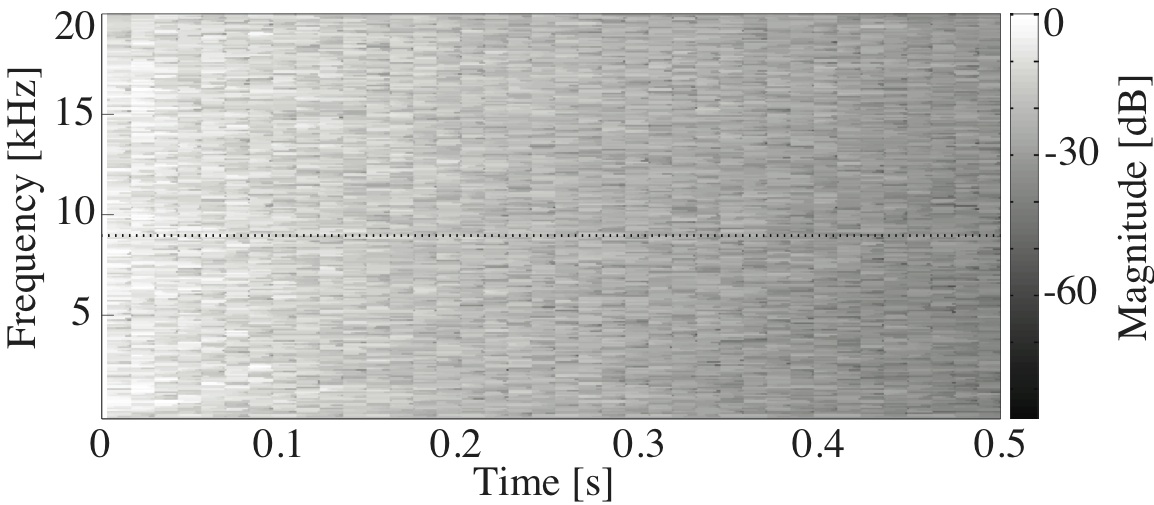
This paper is concerned with an acoustical phenomenon called sweeping echo, which manifests itself in a room impulse response as a distinctive, continuous pitch increase. In this paper, it is shown that sweeping echoes are present (although to greatly varying degrees) in all perfectly rectangular rooms. The theoretical analysis is based on the rigid-wall image solution of the wave equation. Sweeping echoes are found to be caused by the orderly time-alignment of high-order reflections arriving from directions close to the three axial directions. While sweeping echoes have been previously observed in real rooms with a geometry very similar to the rectangular model (e.g. a squash court), they are not perceived in commonly encountered rooms. Room acoustic simulators such as the image method (IM) and finite-difference time-domain (FDTD) correctly predict the presence of this phenomenon, which means that rectangular geometries should be used with caution when the objective is to model commonly encountered rooms. Small out-of-square asymmetries in the room geometry are shown to reduce the phenomenon significantly. Randomization of the image sources' position is shown to remove sweeping echoes without the need to model an asymmetrical geometry explicitly. Finally, the performance of three speech and audio processing algorithms is shown to be sensitive to strong sweeping echoes, thus highlighting the need to avoid their occurrence.
Acknowledgments